
Here, the columns 0 1, 0 2, 0 3, 0 4, 0 5 specify the operator and the rows L 1, L 2, L 3, L 4, L 5 specify which loom is to be used for the particular experiment. If five operators are employed, the necessary set of twenty-five experiments can be specified by means of the 5 × 5 latin square illustrated in the left-hand diagram of Figure 11.5.1. However, by making use of the statistical technique of analysis of variance, a satisfactory test result can be obtained provided that each type of treated yarn is spun once on each loom and also once by each operator. If time were of no account, it would be desirable ideally to test the effect of every treatment with every operator and on every loom. Five looms are available for spinning the yarn and it is believed that both the loom used and the operator employed may affect the final texture of the spun yarn. Suppose that it is required to test the effect of five different treatments on yarn. τ represents the amplitude and usually τ = 10%. Take the negative factor p 1 as an example.įirst determine the factor set related to p 1: M( p 1) = , i = 1, 2, …, r, and set the sampling interval of coupled factors p i as:, p i ∈ M( p 1). The more the sensitivity achieved, the more the possibility that it will have a negative influence on other related factors. This requires sensitivity analysis on the negative factor. If the model is modified to rectify the negative factor, it is possible to influence other factors related to the modified one. Its principle is to decompose the multivariant function into a constant, single-variant function and a combined-variant function, and use the variance of multivariant function and each subitem to calculate the sensitivity of different variants. Sobol's method ( Sobol, 1990) is a global sensitivity analysis method based on variance decomposition, which was proposed by I.M. Ke Fang, Ming Yang, in Model Engineering for Simulation, 2019 5.2 Sobol's Method With constructed distribution in hand, one can further apply the hypercube sample method to generate the final samples. These statistical parameters can then further be used to construct a distribution function, for instance, the normal distribution. The next step is to reduce the number of sampling by calculating the mean, the variance, and the standard deviation of the generated sample. Assume that the uncertain parameter is β and it ranges within, then the first step in this method consists of generating the sampling via the Monte Carlo sampling within. We propose a methodology that combines both the Monte Carlo simulation and the Latin hypercube sampling as follows. However, this Monte Carlo simulation still presents some worth. Monte Carlo hypercube sampling method It was demonstrated that the hypercube sample method was more efficient and less time consuming than the Monte Carlo simulation. Since both methods have limitations and strengths, we propose a new approach that combines both methods the new approach will be called Monte Carlo Hypercube Sampling Method (MCHSM). ) as a step function, one achieves the empirical distribution function of h at the point c. If g ( h ) = H i, one obtains the rth sample moment. If g ( h ) = h, that is, if h is a fixed point for g, then T represents an estimator of. ) is an arbitrary known function and H i = q ( x i ). Let h denote an objective function given by Įfficiency of LHSMC Considers the case that x denotes an n-vectors random variable with p.d.f.In this case, the equal probability spaced values are 0. A 10-run LHS for three normalized variables (range ) with the uniform probability density function (p.d.f.) is listed below. Thus, for given values of N and n, there exist ( N ! ) n − 1 possible interval combinations for an LHS. This set of Nn-tuples is the Latin hypercube sample.
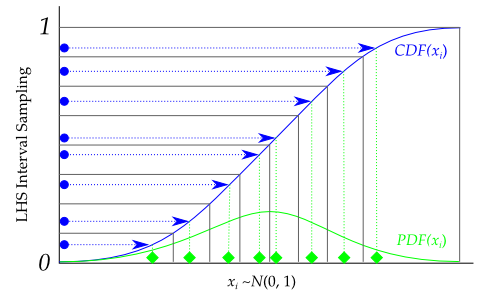
These N pairs are combined in a random manner with the N values of x 3 to form Nn-triplets, and so on, until a set of Nn-tuples is formed. The N values thus obtained for x 1 are paired in a random manner with the N values of x 2. One value from each interval is selected at random with respect to the probability density in the interval. The range of each variable is partitioned into N non-overlapping intervals on the basis of equal probability size 1 / N. As originally described, in the following manner, LHS operates to generate a sample size N from the x variables x 1, x 2, x 3. Moreover, the sample generation for correlated components with Gaussian distribution can be easily achieved. We will only consider the case where the components of x are independent or can be transformed into an independent base. The sampling region is partitioned into a specific manner by dividing the range of each component of x. The Latin Hypercube Sampling (LHS) is a type of stratified Monte Carlo (MC).


 0 kommentar(er)
0 kommentar(er)
